| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- python자료형
- c언어 제어문
- 파이썬 알고리즘 인터뷰
- 코테
- 코딩테스트
- #코린이 #코딩 #할 수 있다
- 그리디
- c언어 기본
- python기초
- 1주차(1)
- 참고X
- git 오류
- 최단거리
- 5장
- python기본
- 도커
- git오류
- DP
- Workbench
- 인스타
- git기초
- 자료구조
- 인텔리제이
- 운체 1주차
- 백준
- c언어
- Git
- 4장
- 데베시 1주차
- 스택
- Today
- Total
하루살이 개발자
[알고리즘] 우선순위 큐 (Priority Queue) 본문
1. 우선순위 큐란?
- 일반적인 큐(Queue)는 First in-First Out 구조이다. (부가적인 조건 없이 먼저 들어온 데이터가 먼저 나가는 구조)
- 우선순위 큐(Priority Queue)는 들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나오는 것이다.
- 우선순위 큐는 힙(Heap)이라는 자료구조를 가지고 구현할 수있다.
- 큐나 스택과 비슷한 자료형이지만, 각 원소들은 우선순위를 가지고 있다.
- 우선순위 큐에서, 높은 우선순위를 가진 원소는 낮은 우선순위를 가진 원소보다 먼저 처리된다. 같은 우선순위를 가진다면, 먼저 들어온 원소를 처리한다.
- 우선순위 큐는 힙(heap)이라는 자료 구조를 통해 구현할 수 있다.
- 우선순위 큐는 최소한 두 가지 연산이 지원되어야 한다.
- 하나의 원소를 우선순위를 지정하여 추가하는 함수(push)
- 가장 높은 우선순위를 가진 원소를 큐에서 제거하고 반환하는 함수(pop)
2. 힙(Heap)이란?
- 완전 이진 트리(Complete Binary Tree)
- 부모 노드의 값이 항상 자식 노드들의 값보다 크거나(Max Heap), 작아야(Min Heap) 한다.
- 힙은 우선순위 큐를 구현하거나, 힙 정렬을 하는 데 사용된다.
- 루트 노드에 있는 값이 최대값, 혹은 최소값이며, 자식 노드들의 값의 위치는 기본적인 조건만 맞추면 된다.
* 직접 연결된 자식-부모 노드 간의 크기만 비교하면 됩니다.
* 힙으로 우선순위 큐를 구현할 때에는 노드에 저장된 값을 우선순위로 봅니다.
따라서 힙은 루트 노드에 우선순위가 높은 데이터를 위치시키는 자료구조가 된다.
그러므로 우선순위 큐를 구현하기에 딱 맞는 자료구조 이기도 합니다. 힙에 저장된 노드를 뺄 때마다 우선순위가 높은 데이터 먼저 빠져나오기 때문입니다.
우선순위 큐를 들어가기 전에 힙 자체에 대해서만 살펴보도록 하겠습니다.
* 최대 힙(Max Heap)은 완전 이진트리이면서, 루트 노드로 올라갈수록 저장된 값이 커지는 구조이다. 우선순위는 값이 큰 순서대로 매긴다.

* 최소 힙(Min Heap)은 완전 이진트리이면서, 루트 노드로 올라갈수록 값이 작아지는 구조이다. 우선순위는 값이 작은 순서대로 매깁니다. 최대 힙이던 최소 힙이던 루트 노드에는 우선순위가 높은 것이 자리잡게 된다.

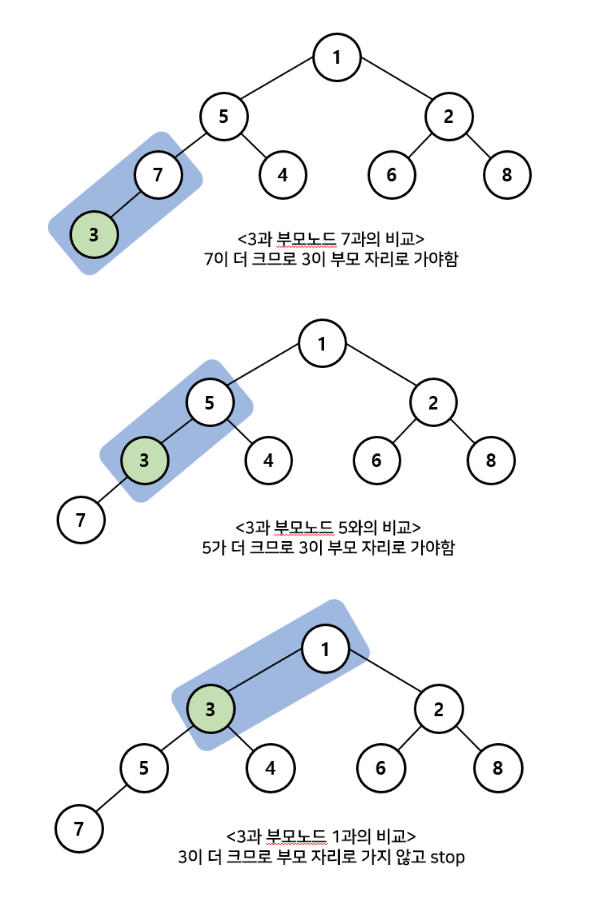
1) 우선순위 큐의 Push
- 맨 끝 위치에 값을 저장
- 부모 노드와 비교하며, 조건을 만족하는 지 확인
- 만족하지 않는다면, 서로 위치를 변경
2) 우선순위 큐의 Pop
- 가장 우선순위가 높은 값을 삭제
- 맨 끝의 노드를 비어있는 루트 노드로 끌어옴
- 루트 노드의 자식 노드들과 값을 비교, 위치 변경
- 위치를 만족할 때까지 자식 노드와 위치를 변경하며 올바른 위치까지 이동

3. 파이썬에서의 우선순위 큐
파이썬에서는 우선순위 큐의 활용을 위해, 모듈을 제공하고 있다
PriorityQueue
from queue import PriorityQueue
q = PriorityQueue()
q1 = PriorityQueue(maxsize=10) # maxsize를 활용하면 크기 제한 가능
put
- .put(item)
q.put(3) # 원소를 넣는 과정
q.put(4)
q.put(1)
q1.put((1, 'apple')) # (우선순위, 값)의 형태로 저장할 수도 있음
get
- .get()
# 원소 삭제 및 반환
q.get() # 1
q1.get()[1] # (우선순위, 값)의 형태에서 값 반환Heapq
자세한 내용은 https://docs.python.org/ko/3/library/heapq.html 참조
- 최소 힙(Min Heap)의 구조
- 모든 k에 대해 heap[k] <= heap[2*k+1] 또는 heap[k] <= heap[2*k+2] 만족
- 가장 작은 요소가 heap[0]에 위치
- 힙을 만들기 위해서는, 초기화된 리스트 []를 사용하거나, heapify를 통해 값이 들어있는 리스트를 힙으로 변환 가능
import heapq
hq = []
push
- heapq.heappush(heap, item)
- 힙의 형태를 유지하면서 item을 push
heapq.heappush(hq, 4)
heapq.heappush(hq, 1)
heapq.heappush(hq, 3)
heapq.heappush(hq, 7)
pop
- heapq.heappop(heap)
- 힙의 형태를 유지하면서 가장 작은 항목을 pop, 반환
- 비어있으면 IndexError 발생
- 반환하지 않고 접근하고 싶다면, heap[0] 활용
heapq.heappop(hq) # 1
heapify
- heapify(x)
- 리스트 x를 선형 시간으로 제자리에서 heap으로 변환
x = [4, 3, 1, 2, 5, 6]
print(x) # [4, 3, 1, 2, 5, 6]
heapq.heapify(x)
print(x) # [1, 2, 4, 3, 5, 6]
4. 구현
import heapq
pq = []
heapq.heappush(pq, 1)
heapq.heappush(pq, 5)
heapq.heappush(pq, 2)
heapq.heappush(pq, 4)
heapq.heappush(pq, 3)
# print(pq) [1, 3, 2, 5, 4]
print(heapq.heappop(pq)) # 1
print(heapq.heappop(pq)) # 2
print(heapq.heappop(pq)) # 3
print(heapq.heappop(pq)) # 4
print(heapq.heappop(pq)) # 5
* 튜플로
import heapq
pq = []
heapq.heappush(pq, (1, 2, 4))
heapq.heappush(pq, (2, 1, 1))
heapq.heappush(pq, (1, 3, 4))
heapq.heappush(pq, (1, 3, 3))
heapq.heappush(pq, (1, 2, 3))
print(heapq.heappop(pq)) # (1, 2, 3)
print(heapq.heappop(pq)) # (1, 2, 4)
print(heapq.heappop(pq)) # (1, 3, 3)
print(heapq.heappop(pq)) # (1, 3, 4)
print(heapq.heappop(pq)) # (2, 1, 1)
[주의] 왜 우선순위 큐는 배열이나 연결리스트로 구현하지 않을까?
1) 배열로 구현한다고 가정
- 우선순위가 높은 순서대로 배열의 가장 앞부분부터 넣는다면, 우선순위가 높은 데이터를 반환하는 것은 맨 앞의 인덱스를 바로 이용하면 되므로 어렵지 않다.
- 우선순위가 중간인 것이 들어가야 하는 삽입 과정에서는 뒤의 데이터까지 인덱스를 모두 한 칸씩 뒤로 밀어야 하는 단점이 있다.
- 최악의 경우 삽입해야 하는 위치를 찾기 위해 모든 인덱스를 탐색해야 합니다. 즉 이 때의 시간 복잡도는 자료가 n개라고 할 때 O(n) 이 된다. → 배열로 구현 시 시간 복잡도 : 삭제는 O(1), 삽입은 O(n)
2) 연결리스트로 구현한다고 가정
- 우선 순위가 높은 순서대로 연결을 시키면, 우선순위가 높은 데이터의 반환은 배열과 마찬가지로 쉽다.
- 하지만 연결리스트 또한 삽입의 과정 또한 배열과 마찬가지로 그 위치를 찾아야 한다. 최악의 경우 맨 끝에까지 가게 된다. → 연결리스트로 구현 시 시간 복잡도 : 삭제는 O(1), 삽입은 O(n)
3) 우선순위 큐를 힙으로 구현한다고 가정
- 힙의 경우 삭제나 삽입 과정에서 모두 부모와 자식 간의 비교만 계속 이루어진다.아래에서 다룰 것입니다)
- 즉, 이진 트리의 높이가 하나 증가할 때마다 저장 가능한 자료의 갯수는 2배 증가하며, 비교 연산 횟수는 1회 증가합니다. 즉 삭제나 삽입 모두 최악의 경우에는 O(log2n) 의 시간 복잡도를 가진다. → 힙으로 구현 시 시간 복잡도 : 삭제는 O(log2n), 삽입은 O(log2n)
- 따라서 배열이나 연결 리스트가 삭제에서는 시간 복잡도의 우위를 점할지라도, 삽입의 시간 복잡도가 힙 기반이 월등하기 때문에, 편차가 심한 배열과 연결리스트보다는 힙으로 구현한다!
Reference
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] union-find 알고리즘 (0) | 2022.02.20 |
|---|---|
| [알고리즘] 소수찾기 - 에라토스테네스의 체 (0) | 2022.02.16 |
| [알고리즘] 최단 경로 알고리즘(1) - 다익스트라(Dijkstra) 알고리즘 (0) | 2022.02.13 |
| [알고리즘_그래프] DFS(깊이 우선 탐색) 예제 (0) | 2022.01.23 |
| [알고리즘] 그래프 탐색 01_DFS(깊이 우선 탐색)/BFS(너비 우선 탐색) (0) | 2022.01.23 |


